#数楽 WolframAlphaで2017についてカンニングしてみた。WolframAlphaは本当に使わない日がない。http://www.wolframalpha.com/input/?i=2017 たとえば【2017^2 = 792^2 + 1855^2】これには気付かなかった。
#数楽 リンク先に書いたことを繰り返します。(1+t)^{1/t}のt→0での極限はeです。これは大学受験生も知っていると思う。それでは(1+t)^{1/t}はどの程度の速さでeに収束するでしょうか?続くhttps://twitter.com/genkuroki/status/776241723244548096 …
#数楽 続き。そのために((1+t)^{1/t}-e)/tのt→0での極限を求めることになったとする。ロピタル脳の人は機械的に分子分母をtで微分して非常に面倒な計算に突入することになります。実はそれでも解けますが、求まるのは極限値だけ。苦労する割に得られるものは少ない。続く
#数楽 続き。「(1+t)^{1/t}がt→0でどのようにeに収束するかを調べよ」は受験云々とは無関係に数学的に極めて自然な問題です。そういう数学的に自然な問題にロピタル脳な人が立ち向かうと滅茶苦茶苦労してほんのちょっとの成果しかあげられない。ロピタル脳になるのは損です。続く
#数楽 続き。数学を教えている人ならみんな知っている基本的な道具にTaylor展開があります。展開が収束しなくても、剰余項付きのTaylorの定理を使うことができるので、展開の収束性はあまり気にしなくてよい。続く
#数楽 (1+t)^{1/t}に二項展開を適用してもかなり面倒なことになります。対数を取ってから対数函数のTaylor展開を使うとすっきり問題が解決。log(1+t)^{1/t}=(1/t)log(1+t)にlog(1+t)=t-t^2/2+O(t^3)を代入すると〜続く
#数楽 続き〜、log(1+t)^{1/t}=1-t/2+O(t^2)なので、(1+t)^{1/t}=e e^{-t/2} e^{O(t^2)}=e(1-t/2+O(t^2))となることが暗算でも確認できます。とても楽ちん。続く
#数楽 続き。受験数学の世界で伝統的に広まっているやり方の多くは中途半端で実用には適さない方法だと思います。ロピタルの定理はその典型例。そんなのやる暇があったら漸近挙動を調べるための基本的な方法を勉強してしまった方が時間の節約になると思う。特別に難しいことではない。続く
#数楽 漸近挙動を調べるときの最初の基本は「指数函数は多項式函数よりも圧倒的に速く増加する」に代表される増大度や減少度のオーダーの違いに関する基本的な知識です。オーダーの違いの階層を意識することが最初の基本。そしてその次の基本はTaylor展開もしくはTayorの定理。
#数楽 結局、受験数学の世界では、昔から教えられて来たことが、手法としての効率の良さとか合理性について何も考えずに、そのまま現在も教えられていたりするんじゃない。しかも「減点されるかもしれない云々」という根拠不明の都市伝説込みで教えられていたりする。これもまた不毛の極致。
#数楽 「本物の知識を地道にかつ効率良く勉強する」ってのが結局のところ最強でかつ楽な道だと思う。そのためには良い先生が必要。特に純粋な若い人達の場合には、価値ある本物の知識を勉強していると確信しているときと、そうでないときでは、モチベーションが段違いになると思う。
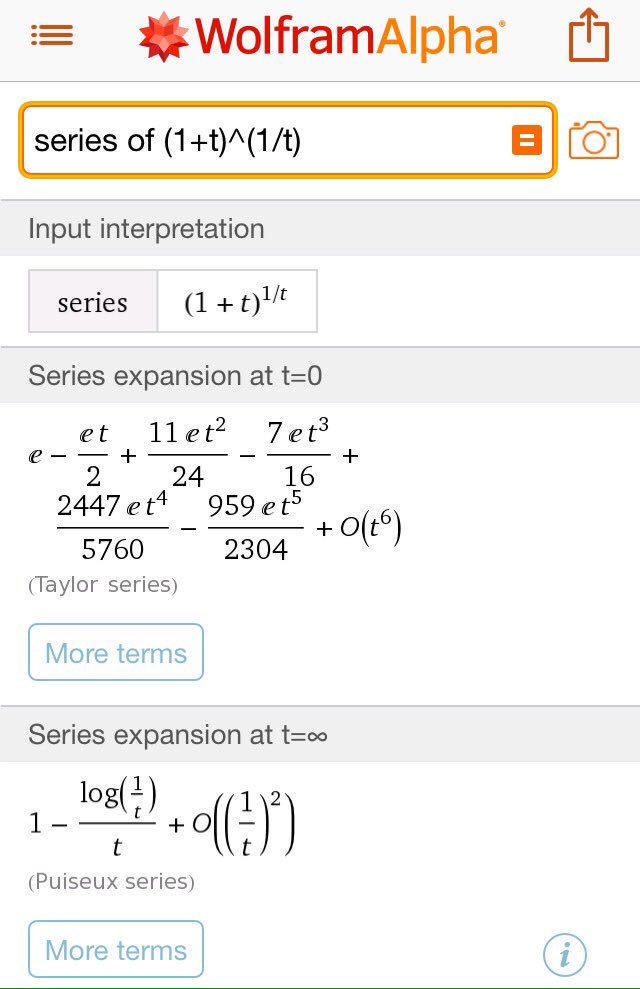
#数楽 (1+t)^(1/t) のt=0付近のグラフはリンク先で見れます→ http://www.wolframalpha.com/input/?i=series of (1+t)^(1/t) …https://twitter.com/beyondDNS/status/822613927179808772 …
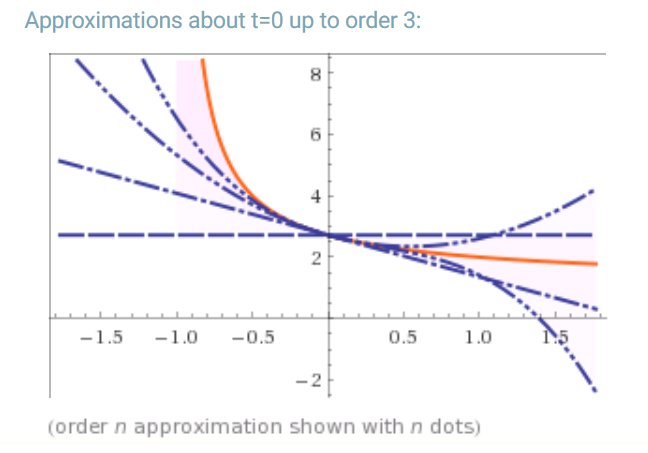
#数楽 (1+t)^(1/t) のt=0付近のグラフオレンジの線が(1+t)^(1/t)のグラフで青の点線はTaylor展開による近似pic.twitter.com/hatuwRhUMq
#数楽 すみません。グラフも引用しておくべきでした。グラフを描くことはとてもよいこと。今ならコンピューターを気軽に利用できる環境が整っているので「必須だ」と言って問題ないと思う。WolframAlphaを使うと勝手にグラフを見せてくれる場合が多い。
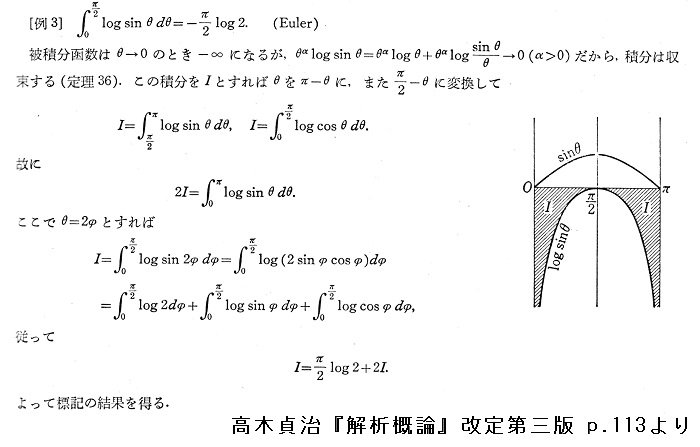
#数楽 添付画像はlog(sin x)の0からπ/2の定積分の計算(高木貞治『解析概論』より)。WolframAlphaを使っていて気づいたのですが、log(sin x)の原始函数はダイログを使って書けるんですね→ http://www.wolframalpha.com/input/?i=\int+log(sin+x)+dx …pic.twitter.com/U0XCu36vPa
#数楽 f(x)=log(sin x)の原始函数はF(x)=(i/2)(x^2 + Li_2(e^(2 i x))) - x log(1 - e^(2 i x)) + x log(sin x) + const.になります。http://www.wolframalpha.com/input/?i=\int+log(sin+x)+dx …
#数楽 dilog Li_2(x)程度は「普通の函数」だと思って良さそうですよね。より一般にpolylogがLi_r(x)=x/1^r+x^2/2^r+x^3/3^r+…と定義されることを知っておくのは損ではないと思う。dilogの量子化はとても面白い。
#数楽 ぎょぎょぎょ。『解析概論』p.112には「∫_0^π (x sin x)/(1+(cos x)^2) dx=π^2/4」という公式が書いてあるのですが、その被積分函数の原始函数もdilogを使って表示できるようですね→http://www.wolframalpha.com/input/?i=\int+(x+sin+x)/(1+(cos+x)^2)+dx …
#数楽 ふうむ。『解析概論』p.112には「∫_0^π (log(1+x))/(1+x^2) dx=(π/8)log 2」という公式も書いてあるのですが、その被積分函数の原始函数もdilogを使って表示できるようです→http://www.wolframalpha.com/input/?i=\int+(log(1+x))/(1+x^2)+dx …
先日、オイラーの元ネタについてツイートしたばかりですhttps://twitter.com/Paul_Painleve/status/820921168664215552 …
#数楽 @Paul_Painleve ああ、なるほど、x log(sin x)の原始函数はtrilogで表示できますね→ http://www.wolframalpha.com/input/?i=\int+x+log(sin+x)+dx …https://twitter.com/Paul_Painleve/status/820922235330269184 …
#数楽 問題:非負の整数nに対して、x^n log(sin x)の原始函数をpolylogたちで表示できることを示せ。http://www.wolframalpha.com/input/?i=\int+x^4+log(sin+x)+dx …
Re:RT #数楽http://www.wolframalpha.com/input/?i=23456789 …23456789 is the hypotenuse of a primitive Pythagorean triple: 23456789^2 = 9341740^2 + 21516339^2
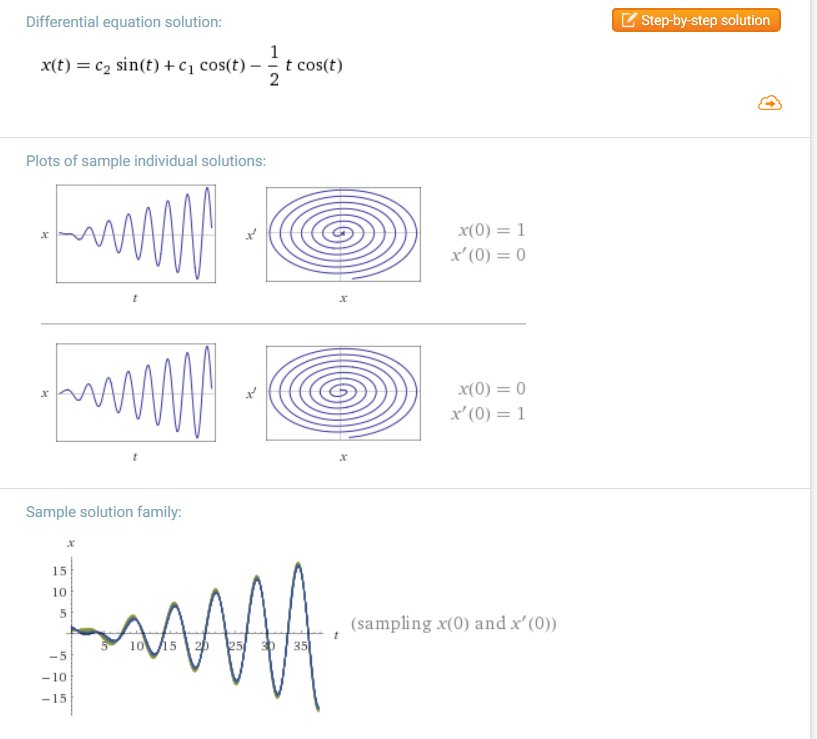
#数楽 WolframAlpha で x''(t)=-x(t)+sin t を解く。振幅がどんどん大きくなる。http://www.wolframalpha.com/input/?i=solve+x''=-x+sin+t …pic.twitter.com/fS5HuhMX3F
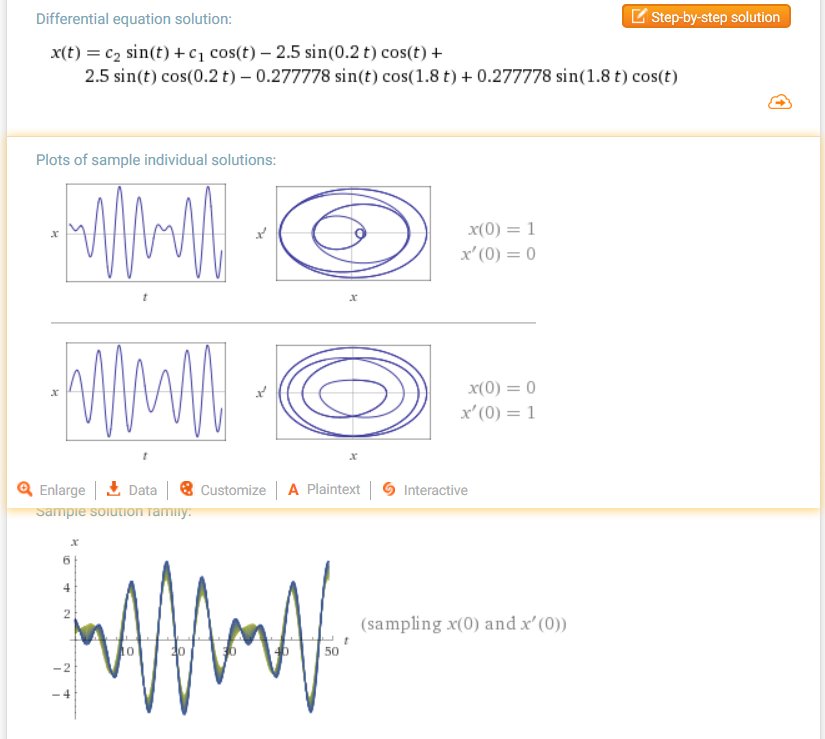

#数楽 不定積分 ⌠ log(sin x) dx などが多重対数で書けること。添付画像は WolframAlpha で計算した結果。pic.twitter.com/YSvwnwAsaQ

#数楽 log(1+x)/(1+x^2) や (x sin x)/(1+cos^2 x) の不定積分もダイログを使って表せる。添付画像はWolframAlphaを使って計算した結果。pic.twitter.com/gXjcNX1v2s
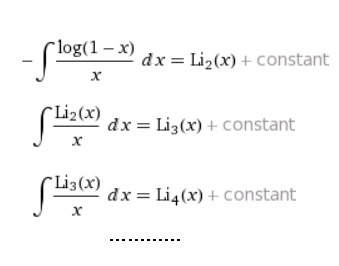

#数楽 f_r(z)=Li_r(e^z)=(r重のポリログにe^zを代入したもの、Li_1(x)=-log(1-x))とおくと、⌠ f_r(z) dz = f_{r+1}(z) + const.pic.twitter.com/Ei1Edu2B1f
#数楽 続き。sin x=(e^{ix}-e^{-ix})/(2i)なので⌠log(sin x)dxの計算は公式-⌠log(1-e^z)dz=Li_2(z)+const.に帰着します。これがlog(sin x)の不定積分にダイログが出て来る理由です。
#数楽 f_{r+1}の導函数がf_rのとき部分積分の繰り返しによって、⌠z^n f_r(z)dz=z^n f_{r+1}(z)-nz^{n-1}f_{r+2}(z)+…+(-1)^n n! f_{r+n+1}(z).これをf_1(z)=-log(1-e^z)に~続く
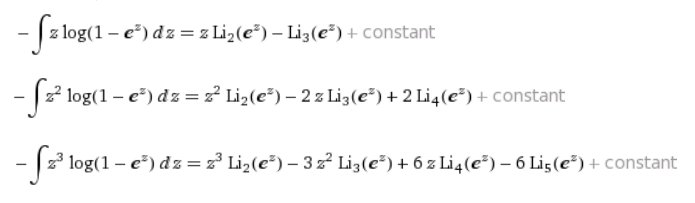
#数楽 続き~適用すれば、f_r(z)=Li_r(e^z)なので、-⌠z^n log(1-e^z)dz=z^n Li_2(e^z)-nz^{n-1}Li_3(e^z)+…+(-1)^n n! Li_{n+2}(e^z).pic.twitter.com/JEQoOS7JaO

#数楽 続き。x log(sin x)の原始函数をダイログとトリログで表わす公式からはEuler全集E432§21にある公式が得られます。Eulerさんがどんな感じの世界を見ていたかが少しわかった気分になりました。やはり、原始函数の明示的な公式があるなら書き下しておいた方がよい!pic.twitter.com/ywVFaiUcoW

#数楽 続き。x^2 log(sin x)で同様のことをやると、実部から⌠_0^{π/2} log(sin x)dx=(3π/16)ζ(3)-(π3/24)log 2が得られ、虚部=0からζ(4)=π^4/90の独立な証明が得られます。pic.twitter.com/eNtkTF4Szr
#数楽 https://twitter.com/genkuroki/status/845586032598773760 …訂正:リンク先の添付画像中のAlframはWolframが正しい。
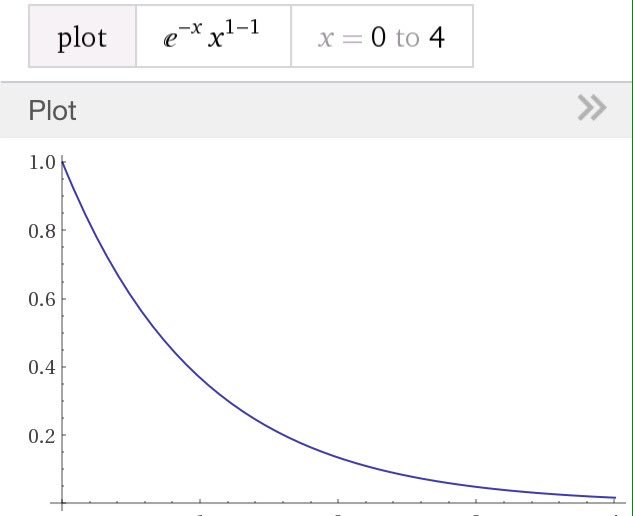
#数楽 添付画像は平均1の指数分布のグラフです。λ=1/μ=1の場合。正規化していないので、縦軸の目盛りは無視来てください。保有するお金の量が小さいほど確率が高くなる。現実の貯金の分布もこんな感じ。pic.twitter.com/D9p1DJeerG
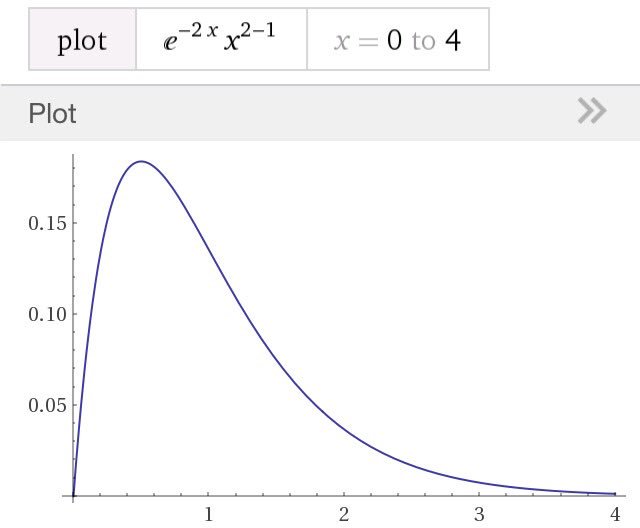
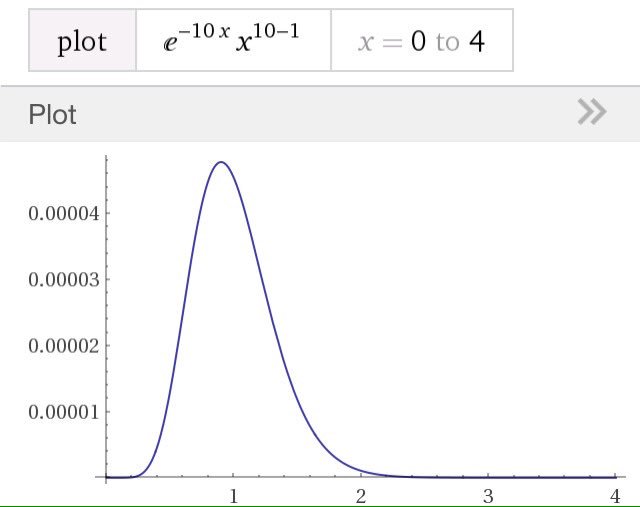
#数楽 平均は1のままだが、λ=2としたガンマ分布のグラフ。λ=1/μ=2の場合。お金を全然持っていない人が減っている。縦軸の目盛りは無視してください。pic.twitter.com/iR5mmUrNMp

#数楽 添付画像はWolframAlphaに教えてもらった log(sin x) の原始函数F(x)が実際に原始函数であることの証明。微分するだけなのですが、初心者はそこでつまるかもしれないので、念のためにノートの画像を公開。pic.twitter.com/z2JnhA8Ysh
#数楽 ちなみにWolframAlphaさんに不定積分 ∫du/(1+u^{1/s}) について効くと超幾何函数での表示を教えてくれます。http://www.wolframalpha.com/input/?i=\int+du/(1+u**{1/s} …)+
#数楽 B(p,q)=∫_0^∞ t^{p-1}dt/(1+t)^{p+q}なのですが、被積分函数の不定積分についてWolframAlphaさんに尋ねるとやはり超幾何函数表示を教えてくれます。http://www.wolframalpha.com/input/?i=\int+t^{p-1}dt/(1+t)^{p+q} …
#数楽 自明な訂正。リンク先の左辺の⌠_0^{π/2} log(sin x)dxはもちろん正しくは⌠_0^{π/2} x^2 log(sin x)dxです。x^2を書き忘れた。いつもごめんなさい。https://twitter.com/genkuroki/status/845613007212240896 …
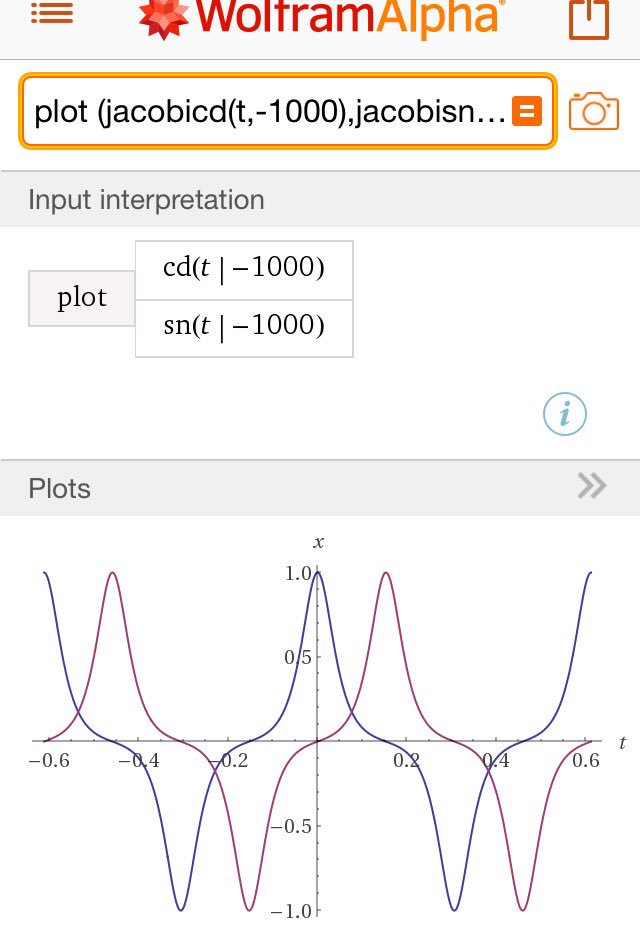
#数楽 ヤコビの楕円函数のプロットはWolframAlphaを使えば一発でできる。cd(t|k^2),sn(t|k^2)はjacobicd(t,k^2),jacobisn(t,k^2).http://www.wolframalpha.com/input/?i=plot%20(jacobicd(t,-1000),jacobisn(t,-1000)) …pic.twitter.com/o0rV8DpWRB
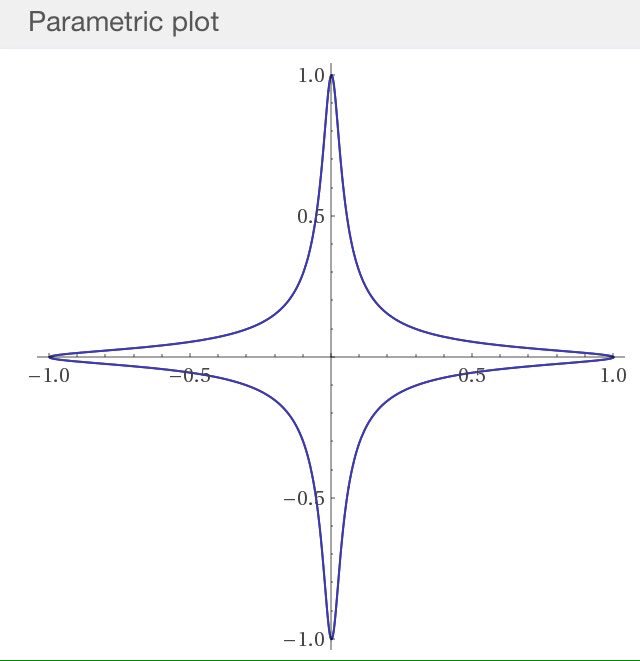
#数楽 スクショの続き。(x,y)=(cd t, sn t)をプロットとするとEdwards曲線x^2+y^2=1+k^2x^2y^2が得られます。添付画像はk^2=-1000の場合。pic.twitter.com/sJvJRNsY3C
#数楽 函数や曲線の様子を見たければまず最初にWolframAlphaを使うのがよいと思う。数学的に初等的はケースではGeoGebraも便利。何も知らない状態から数時間あればリンク先のようなことができます。https://www.geogebra.org/m/XjJ2yPhp
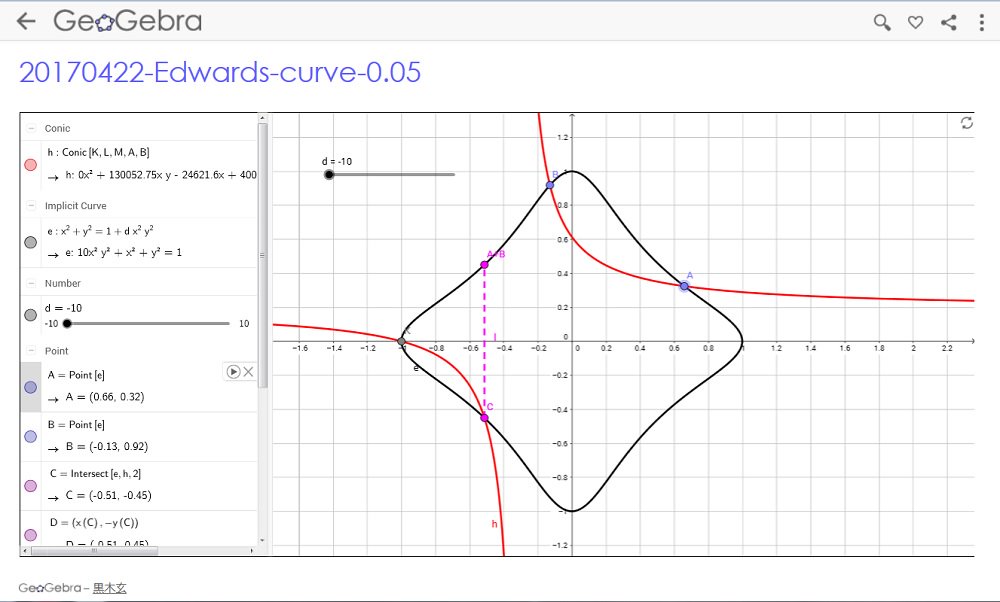
#数楽 GeoGebraを使った楕円曲線のEdwards formの加法公式のプロットの例のスクリーンショット(GeoGebraについて何も知らなくても数時間あればこの程度の初等的なことなら可能)https://www.geogebra.org/m/XjJ2yPhp pic.twitter.com/dC4PG1cm9H
#数楽 続き。私は初めて触るこの手の道具を平均より早く使える方だと思う。それにもかかわらず、数時間かけてその程度のことしかできないとも言える。GeoGebraのような道具は、数学を教える側ではなく、教わる側が使用しなければ教育的効果は小さいと思うのですが、現実は厳しいかも。
#数楽 WolframAlpha https://www.wolframalpha.com/ で図やグラフを描くための使い方を覚えるために必要な時間は短い。英語の説明を読めないとつらい。例を幾つか知っていて数式の入力の仕方を知っていればWolframAlphaが勝手に図を描いてくれる。
#数楽 リンク先はガンマ函数が入っている式を初めて見た人がWolframAlphaに「Γ(s)=?」とテキトーに質問してみた場合の結果です。大量の情報がてんこ盛りで返って来る。https://www.wolframalpha.com/input/?i=�%93(s)=? …
#数楽 行列[ 1 2 ][ 2 3 ]は{{1,2},{2,3}}と入力する。やはりその行列関連の大量の情報を教えてくれる。https://www.wolframalpha.com/input/?i={%7B1,2},{2,4}} …
#数楽 右上に小さくπ/2と書きたい場合には^{π/2}と書きます。右下に小さく0と書く場合には_0と書きます。リンク先は0からπ/2まで積分です。int_0^{π/2} (sin x)^n dxhttps://www.wolframalpha.com/input/?i=int_0^{π/2}+(sin+x)^n+dx …
#数楽 WolframAlphaの使用例についてはリンク先の返答連鎖で紹介しているまとめを見て下さい。https://twitter.com/genkuroki/status/853142593181425664 …



